안녕하세요. 회사와 함께 성장하고 싶은 KOSE입니다.
이번 포스팅은 프로그래머스 표 병합을 자바로 푼 과정을 정리하도록 하겠습니다.
문제 출처: https://school.programmers.co.kr/learn/courses/30/lessons/150366
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
1. 풀이 소스
import java.util.*;
import static java.lang.Integer.parseInt;
class Solution {
public String[] solution(String[] commands) {
Matrix matrix = new Matrix();
return matrix.apply(commands);
}
}
class Matrix {
static final int RANGE = 2501;
int[] parent = new int[RANGE]; // 인덱스에 부모 인덱스를 넣기위한 일차원 배열
String[] values = new String[RANGE]; // 셀의 값을 넣기 위한 배열
Matrix() { // 초기화
for (int i = 1; i < RANGE; i++) {
parent[i] = i;
values[i] = "";
}
};
int find(int a) { // 재귀로 루트 인덱스를 찾기 위한 과정
if (parent[a] == a) return a; // 만약 루트 노드가 없다면 자기 자신 인덱스 이므로 리턴
else return parent[a] = find(parent[a]); // 재귀 시작 후 ex a[1] = 3 -> a[3] = 4 -> a[4] = 4 라면 종료 후 4 반환
}
void union(int a, int b) {
if (a != b) parent[b] = a; // parent[b] = a 로 설정하면서 union 실행
}
// parent[7] = 4 --> parent[13] 즉 리프 노드부터 parent[4] = 4 까지 연결됌
int convertIndex(int row, int col) {
return 50 * (row - 1) + col; // row = 1, y = 1 -> 1 // row = 2, y = 1 -> 51
}
void update(int r, int c, String value) {
int idx = convertIndex(r, c);
values[find(idx)] = value; // 루트 노드를 찾아서(find) 반환 후 루트 노드의 values를 value 변경
}
void update(String before, String after) {
for (int i = 1; i < RANGE; i++) {
if (before.equals(values[i])) values[i] = after; // 루트 노드가 기록되므로 루트 노드의 value를 변경
}
}
void merge(int r1, int c1, int r2, int c2) {
if (r1 == r2 && c1 == c2) return; // 병합할 위치가 동일하면 종료
int idx1 = convertIndex(r1, c1); // 병합할 대상
int idx2 = convertIndex(r2, c2); // 병합될(할) 대상
int root1 = find(idx1); // 병합할 대상의 루트 노드 번호
int root2 = find(idx2); // 병합될(할) 대상의 루트 노드 번호
if (root1 == root2) return; // 두 루트 노드가 같다면 이미 병합되어 있는 노드임
String root = values[root1].isBlank() ? values[root2] : values[root1]; // root1의 값이 "" 라면, root2를 기준으로 병합
values[root2] = ""; // root2는 값이 있더라도, root1을 기준으로 병합될 예정이므로 ""
union(root1, root2); // root1 으로 병합
values[root1] = root; // root1의 value를 root1 혹은 root2가 values에 가지고 있던 값으로 업데이트
}
void unmerge(int r, int c) {
int idx = convertIndex(r, c);
int root = find(idx); // 인덱스가 연결된 루트 노드
String rootValue = values[root];
values[root] = ""; // 루트 노드에 값을 ""로 바꿈으로써 병합되어 있던 셀들이 값을 잃음
values[idx] = rootValue; // 선택된 노드에 rootValue를 참조 (만약 값이 있다면 병합을 해제하면 해당 포인트가 값을 얻음)
List<Integer> dels = new ArrayList<>();
for (int i = 1; i < RANGE; i++) {
if (find(i) == root) { // find(i)로 루트 노드로 연결된 노드를 전부 탐색
dels.add(i);
}
}
for (Integer i : dels) {
parent[i] = i; // 해당 인덱스를 자기 자신으로 바꿈으로써 연결 노드 전부 제거
}
}
String print(int r, int c) {
int idx = convertIndex(r, c);
int root = find(idx);
if (values[root].isBlank()) return "EMPTY";
return values[root]; // 루트 노드의 값을 출력 = 병합된 노드의 루트 노드의 값
}
String[] apply(String[] commands) {
List<String> result = new ArrayList<>();
for (String command : commands) {
String[] cmds = command.split(" ");
String cmd = cmds[0];
String v1 = cmds[1];
String v2 = cmds[2];
if (cmds.length >= 4) {
String v3 = cmds[3];
if (cmds.length == 5) merge(parseInt(v1), parseInt(v2), parseInt(v3), parseInt(cmds[4])); // merge
else update(parseInt(v1), parseInt(v2), v3); // update 오버로딩
} else {
if (cmd.equals("UPDATE")) update(v1, v2); // update 오버로딩
else if (cmd.equals("UNMERGE")) unmerge(parseInt(v1), parseInt(v2)); // unmerge
else result.add(print(parseInt(v1), parseInt(v2))); // print
}
}
return result.toArray(new String[0]);
}
}
2. 풀이 중점
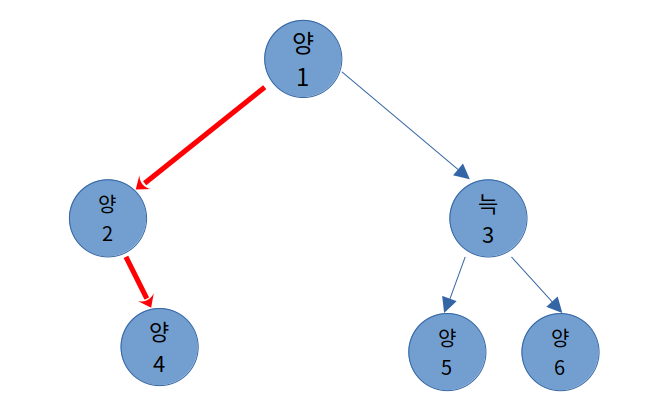
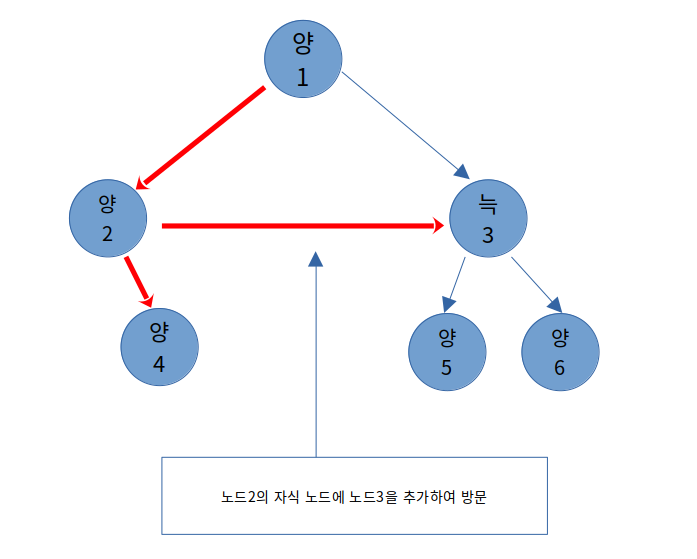
해당 문제는 Union - Find를 활용하여 문제를 해결하는 방법이 있습니다. Union - Find 방법은 재귀적으로 루트 노드를 찾은 후 루트 노드끼리 병합하여 하나의 연결 관계를 만드는 방법입니다.
가령 다음의 배열이 있습니다.
a[0] = 0, a[1] = 1, a[2] = 2, a[3] = 3
여기서 a[0] 과 a[1] 를 연결된 하나의 집합으로 만들고 싶다면 연결관계를 설정할 수 있는 배열을 하나 생성한 후 (p 배열)
p[0] = 1, p[1] = 1 을 처리하여 0 번째 인덱스에 1을 넣음으로써 1이 루트 노드가 되고 두 노드는 재귀식으로 연결관계를 파악할 수 있습니다.
이 문제도 다음과 같이 find(), union() 메서드를 선언하여 먼저 재귀 방법으로 root 노드를 찾은 후, 두 root 노드를 병합하는 과정을 수행할 수 있습니다.
이후, 병합 해제는 루트 노드를 찾은 후, 루트 노드의 value를 ""으로 처리하여 값을 지웁니다. 이후, 재귀로 루트 노드를 가리키는 노드를 찾기 위해 find(i)를 하여 루트 노드라면 해당 값을 자신의 인덱스로 업데이트 합니다.
자세한 설명은 다른 풀이와 마찬가지로 주석으로 처리하였습니다.!

이상으로 표 병합 문제를 마치도록 하겠습니다. 감사합니다.!!!
'Algorithm' 카테고리의 다른 글
| [Algorithm] 프로그래머스 - 모두 0으로 만들기 자바 풀이 (0) | 2023.05.02 |
|---|---|
| [Algorithm] 프로그래머스 - 주차 요금 계산 (0) | 2023.05.01 |
| [Algorithm] 프로그래머스 - 미로 탈출 명령어 자바 풀이 (0) | 2023.04.29 |
| [Algorithm] 프로그래머스 - 두 큐 합 같게 만들기 자바 풀이 (0) | 2023.04.29 |
| [Algorithm] 프로그래머스 - 양궁대회 자바 풀이 (0) | 2023.04.29 |