안녕하세요. 회사와 함께 성장하고 싶은 KOSE입니다.
이번 포스팅은 백준 SW 기출문제 드래곤 커브 자바 풀이를 진행하고자 합니다.
문제 출처:https://www.acmicpc.net/problem/15685
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커
www.acmicpc.net
1. 풀이 소스:
import java.util.*;
import java.io.*;
import static java.lang.Integer.parseInt;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = parseInt(br.readLine());
DragonCurve curve = new DragonCurve();
for (int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
curve.setMap(parseInt(st.nextToken()), parseInt(st.nextToken()),
parseInt(st.nextToken()), parseInt(st.nextToken()));
}
curve.build();
System.out.println(curve.getSquare());
}
}
class DragonCurve {
boolean[][] map = new boolean[101][101]; // 0 ~ 100 까지 유효한 좌표로 드래곤 커브가 된 좌표
List<Start> starts = new ArrayList<>(); // 드래곤 커브 시작점
void setMap(int x, int y, int dir, int g) {
starts.add(new Start(x, y, dir, g));
}
// 0: x++, 1: y--, 2: x--, 3: y++
void build() {
for (Start start : starts) {
List<Point> nowPoints = new ArrayList<>(); // 드래곤 커브로 재귀 형태로 회전할 리스트
nowPoints.add(new Point(start.x, start.y)); // 시작점 입력으로 추가
map[start.x][start.y] = true; // 시작점 드래곤 커브에 true
int referX = 0; // 90도 시계방향으로 회전시킬 기준점이 되는 x 좌표
int referY = 0;
switch (start.dir) {
case 0:
referX = start.x + 1;
referY = start.y;
break;
case 1:
referX = start.x;
referY = start.y - 1;
break;
case 2:
referX = start.x - 1;
referY = start.y;
break;
case 3:
referX = start.x;
referY = start.y + 1;
break;
}
map[referX][referY] = true;
Point refer = new Point(referX, referY);
nowPoints.add(refer);
doCurve(1, start.g, nowPoints); // 재귀 실행
}
}
// 특정 점을 기준으로 시계 방향 회전
// x = a + (b - y)
// y = b - (a - x)
void doCurve(int k, int g, List<Point> nowPoints) { // 참조 #1
if (k == g + 1) return; // 만약 드래곤 커브 세대가 끝이나면 종료
Point refer = nowPoints.get(nowPoints.size() - 1); // 마지막 입력은 모두 참조점이 됨
int prePointIdx = nowPoints.size() - 2; // 참조점을 제외하고 회전시킬 인덱스 (계속 리스트에 추가하므로 인트값을 설정 해야 함)
for (int i = prePointIdx; i >= 0; i--) { // 내림차순 인덱스로 설정 참조 #2
Point p = nowPoints.get(i);
int nextX = refer.x + (refer.y - p.y); // 공식 적용
int nextY = refer.y - (refer.x - p.x);
map[nextX][nextY] = true;
nowPoints.add(new Point(nextX, nextY)); // 다음 좌표 리스트에 추가
}
doCurve(k + 1, g, nowPoints); // 재귀 실행
}
int getSquare() {
int result = 0;
for (int row = 0; row < 100; row++) {
for (int col = 0; col < 100; col++) {
if (map[row][col] && map[row][col + 1] &&
map[row + 1][col] && map[row + 1][col + 1]) // 0 ~ 99까지 순회하며 4개의 좌표가 모두 true라면 정사각형 가능
result++;
}
}
return result;
}
static class Start {
int x; // x 좌표
int y; // y 좌표
int dir; // 방향성
int g; // 세대
Start (int x, int y, int dir, int g) {
this.x = x;
this.y = y;
this.dir = dir;
this.g = g;
}
}
static class Point {
int x;
int y;
Point (int x, int y) {
this.x = x;
this.y = y;
}
}
}
2. 풀이 중점 사항
참조#1
특정 좌표를 기준으로 90도 시계방향 회전은 행렬의 회전을 이용할 수 있습니다.
이전에 AI 공부할 때, 행렬 회전 공식을 암기했던 적이 있는데, 이번에 쓰이게 되어서 요긴하게 잘 쓸 수 있었던 것 같습니다.
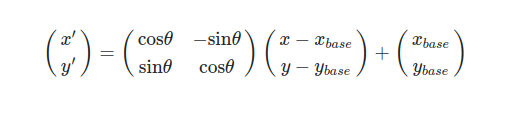
예를 들어 (4, 2)가 회전해야 하는 점이고, 기준점이 (4, 1)이라면 다음의 공식으로 구할 수 있습니다.
- sin90은, 1, 코사인90은 0입니다.
- Xnew = 0 * (4 - 4) + -1 * (2 - 1) = -1, Ynew = 1 * (4 - 4) + 0 * (2 - 1) = 0 인 2 by 1 행렬을 구할 수 있습니다.
- x' = -1 + 4 = 3, y' = 0 + 1 = 1
- 행렬 계산으로 인해 두 행렬을 계산하면 (3, 1)을 구할 수 있습니다.
따라서 이를 일반화 처리하면
int nextX = -(y - refer.y) + refer.x;
int nextY = (x - refer.x) + refer.y;
--------------------------
int nextX = refer.x + (refer.y - y);
int nextX = refer.y - (refer.x - x);로 공식을 구할 수 있습니다.
참조#2
만약 처리해야하는 값이 리스트에
0, 1가 있습니다.
1은 참조점이므로 0만 회전하여 나온 값이 2라면,
0 -> 2 로 리스트에 담기게 됩니다.
현재 리스트: 0, 1, 2
참조점 2를 제외하고 내림차순으로 순회를 하면,
회전을 해서 나온 결과가
1 -> 3,
0 -> 4라고 하겠습니다,
현재 리스트: 0, 1, 2, 3, 4
참조점 4를 제외하고 다시 회전을 진행하면 0, 1, 2, 3, 4, 5, 6, 7, 8
즉, 최종적으로 가장 마지막에 끝나는 인덱스는 처음 리스트 0에 의해 회전한 값이 설정되게 됩니다.
따라서, 내림차순으로 순회하되, 하나씩 리스트에 추가하고 항상 마지막에 추가된 값을 다시 참조점으로 설정할 수 있습니다.
Point refer = nowPoints.get(nowPoints.size() - 1); // 마지막 입력은 모두 참조점이 됨
int prePointIdx = nowPoints.size() - 2; // 참조점을 제외하고 회전시킬 인덱스 (계속 리스트에 추가하므로 인트값을 설정 해야 함)
for (int i = prePointIdx; i >= 0; i--) { // 내림차순 인덱스로 설정 참조 #2
Point p = nowPoints.get(i);
int nextX = refer.x + (refer.y - p.y); // 공식 적용
int nextY = refer.y - (refer.x - p.x);
map[nextX][nextY] = true;
nowPoints.add(new Point(nextX, nextY)); // 다음 좌표 리스트에 추가
}
따라서, 참조점을 설정한 후, 참조점보다 하나 적은 인덱스부터 내림차순 하여 회전한 값을 다시 리스트에 넣는 방법을 적용할 수 있습니다.
재귀로 인해 세대보다 하나가 커질 때까지 계속 드래곤 커브를 생성할 수 있습니다.
이상으로 드래곤 커브 자바 풀이를 마치도록 하겠습니다.
감사합니다.!!
회전 행렬 자료 출처: https://gaussian37.github.io/math-la-rotation_matrix/
'Algorithm' 카테고리의 다른 글
| [Algorithm] SW 기출문제 - 인구 이동(16234) 자바 풀이 (2) | 2023.05.10 |
|---|---|
| [Algorithm] SW 기출문제 - 치킨 배달(15686) 자바 풀이 (2) | 2023.05.09 |
| [Algorithm] SW 기출문제 - 사다리 조작(15684) 자바 풀이 (0) | 2023.05.08 |
| [Algorithm] SW 기출문제 - 감시(15683) 자바 풀이 (2) | 2023.05.08 |
| [Algorithm] SW 기출문제 - 톱니바퀴(14891) 자바 풀이 (0) | 2023.05.07 |